کتاب جبر خطی پیشرفته برای مهندسین با استفاده از نرم افزار MATLAB

جبر خطّی شاخه‌ای از ریاضیات است که به بررسی و مطالعه ماتریس ها، بردارها، فضاهای برداری (فضاهای خطّی)، تبدیلات خطی، و دستگاه‌های معادلات خطی می‌پردازد. جبر خطّی کاربردهای فراوان و گوناگونی در ریاضیات و محاسبات گسسته دارد. علاوه بر کاربردهای آن در زمینه‌هایی از خود ریاضیات همانند جبر مجرد، آنالیز تابعی، هندسه تحلیلی، و آنالیز عددی، جبر خطّی استفاده‌های وسیعی نیز در فیزیک، مهندسی، علوم طبیعی، و علوم اجتماعی پیداکرده است. این درس شامل موضوعاتی است که در یک درس جبر خطی دانشگاهی بررسی می شود که شامل فضاهای برداری، تبدیلات خطی، مقدار یکه و بردار یکه،‌ دستگاه معادلات خطی می باشد...

دانلود کتاب در زمینه متلب

حل کردن مشکلات با استفاده از نرم افزار متلب

راهنمای پیشرفته متلب، مثال های عملی در علوم و مهندسی

مقدمه ای بر محاسبات علمی با نرم افزار متلب

کتاب جبر خطی پیشرفته برای مهندسین با استفاده از نرم افزار متلب (Advanced Linear Algebra for Engineers with MATLAB)، مشتمل بر 6  فصل، 367 صفحه، با فرمت pdf، همراه با تصاویر، به زبان انگلیسی، به ترتیب زیر گردآوری شده است:

Chapter 1: Matrices, Matrix Algebra, and Elementary, Matrix Operations

• Introduction
• Basic Concepts and Notation
• Matrix Algebra
• Elementary Row Operations
• Solution of System of Linear Equations
• Matrix Partitions
• Block Multiplication
• Inner, Outer, and Kronecker Products

Chapter 2: Determinants, Matrix Inversion and Solutions to Systems of Linear Equations

• Introduction
• Determinant of a Matrix
• Matrix Inversion
• Solution of Simultaneous Linear Equations
• Applications: Circuit Analysis
• Homogeneous Coordinates System
• Rank, Null Space and Invertibility of Matrices
• Special Matrices with Applications
• Derivatives and Gradients

Chapter 3: Linear Vector Spaces

• Introduction
• Linear Vector Space
• Span of a Set of Vectors
• Normed Vector Spaces
• Inner Product Spaces
• Orthogonality
• Matrix Factorization

Chapter 4: Eigenvalues and Eigenvectors

• Introduction
• Matrices as Linear Transformations
• Eigenvalues and Eigenvectors
• Matrix Diagonalization
• Special Matrices
• Singular Value Decomposition
• Numerical Computation of Eigenvalues and Eigenvectors
• Properties of Eigenvalues and Eigenvectors of Different Classes of Matrices
• Applications

Chapter 5: Matrix Polynomials and Functions of Square Matrices

• Introduction
• Matrix Polynomials
• Cayley–Hamilton Theorem
• Functions of Matrices
• The State Space Modeling of Linear Continuous-time Systems
• State Space Representation of Discrete-time Systems
• Controllability of LTI Systems
• Observability of LTI Systems

Chapter 6: Introduction to Optimization

• Introduction
• Stationary Points of Functions of Several Variables
• Least-Square (LS) Technique
• Total Least-Squares
• Eigen Filters
• Stationary Points with Equality Constraints

Artifical Neural Network - ANN

MATLAB Video

MATLAB Project

جهت بر لینک زیر کلیک نمایید:

کتاب جبر خطی پیشرفته برای مهندسین با استفاده از نرم افزار MATLAB

اگر به فراگیری مباحث مشابه مطلب بالا علاقه‌مند هستید، آموزش‌هایی که در ادامه آمده‌اند نیز به شما پیشنهاد می‌شوند:

آموزش کاربردی نرم افزار متلب دانشگاه صنعتی اصفهان

کاربرد کامپیوتر در مهندسی (نرم افزار متلب)

متلب زبان محاسبات فنی (Version 5)

آموزش کاربردی نرم افزار متلب (Matlab Application Training)

اصول کار و برنامه نویسی با متلب MATLAB Programming

تجزیه و تحلیل عددی با استفاده از متلب (Numerical Analysis using MATLAB)

SIMULINK، شبیه سازی سیستم دینامیکی برای MATLAB

برنامه نویسی متلب برای مهندسین (Matlab Programming for Engineers)

کتاب تانسورها (ریاضیات نظریه نسبیت و مکانیک پیوسته)

این کتاب به تجزیه و تحلیل انواع مختلف تانسورها می پردازد. فصل اول این کتاب به جبر تانسوری یا به عبارت دیگر به جبر چند بعدی در یک میدان عمومی (F) مربوط می شود. فصل دوم زمینه جبری را به مجموعه ای از اعداد حقیقی (R) محدود می نماید. سایر فصول کتاب در ادامه پایین قابل مشاهده و پیگیری می باشد. بطور خلاصه این کتاب در تکمیل مطالب مربوط به فصل تانسورها که در درس مکانیک محیط های پیوسته بیان می گردد می تواند مفید واقع گردد...

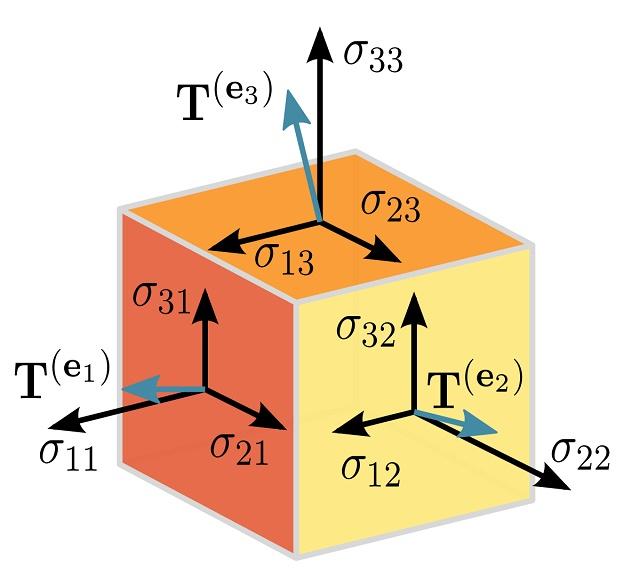
کتاب تانسورها - ریاضیات نظریه نسبیت و مکانیک پیوسته (Tensors - The Mathematics of Relativity Theory and Continuum Mechanics)، مشتمل بر 300 صفحه، در 7 فصل، با فرمت PDF، به زبان انگلیسی، همراه با مثال ها و تمرینات متعدد به ترتیب زیر گردآوری شده است:

Chapter 1: Finite Dimensional Vector Spaces and Linear Mappings

• Fields
• Finite-Dimensional Vector Spaces
• Linear Mappings of a Vector Space
• Dual or Covariant Vector Spaces

Chapter 2: Tensor Algebra

• Second-Order Tensors
• Higher Order Tensors
• Exterior or Grassmann Algebra
• Inner Product Vector Spaces and the
• Metric Tensor

Chapter 3: Tensor Analysis on a Differentiable Manifold

• Differentiable Manifolds
• Tangent Vectors, Cotangent Vectors, and Parametrized Curves
• Tensor Fields over Differentiable Manifolds
• Differential Forms and Exterior Derivatives

Chapter 4: Differentiable Manifolds with Connections

• The Affine Connection and Covariant Derivative
• Covariant Derivatives of Tensors along a Curve
• Lie Bracket, Torsion, and Curvature Tensor

Chapter 5: Riemannian and Pseudo-Riemannian Manifolds

• Metric Tensor, Christoffel Symbols and Ricci Rotation Coefficients
• Covariant Derivatives and the Curvature Tensor
• Curves, Frenet Serret Formulas and Geodesics
• Special Coordinate Charts

Chapter 6: Special Riemannian and Pseudo-Riemannian Manifolds

• Flat Manifolds
• The Space of Constant Curvature
• Einstein Spaces
• Conformally Flat Spaces

Chapter 7: Hypersurfaces, Submanifolds, and Extrinsic Curvature

• Two-Dimensional Surfaces Embedded in a Three Dimensional Space
• (N −1)-Dimensional Hypersurface
• D-Dimensional Submanifolds

جهت دانلود کتاب تانسورها - ریاضیات نظریه نسبیت و مکانیک پیوسته (Tensors - The Mathematics of Relativity Theory and Continuum Mechanics)، بر لینک زیر کلیک نمایید:

کتاب تانسورها (ریاضیات نظریه نسبیت و مکانیک پیوسته)